The gain block allows to amplify an input signal. In general, the input signal is of type matrix and hence, the gain will have to be a matrix as well. However, the type of the input signal and the output signal must be the same. When the gain block is disabled the output is equal to the input. When declaring a gain block you have to make sure that the gain matrix multiplied with the input type produces a result with the same type as the input type.

The following lines show various examples.

Gain<Matrix<2,1>, Matrix<2,2>> g1({1,2.5,-1,-0.5});  // result will be of type Matrix<2,1>

The first template parameter denotes the type of the input and output signal. The second template parameter is the type of the gain, which here is a 2×2-matrix.

Gain<Matrix<1,2>, Matrix<2,2>> g1({1,2.5,-1,-0.5});  // not allowed

This is not allowed because the multiplication of two matrices with the first having dimensions of [2,2] and the second of [1,2] is not defined. If a Gain block is declared with a single value each element of the input vector is multiplied with this value.

Gain<Vector2> g2(10);
Gain<Vector2, double> g3(10);   // this is the same

Another useful operation is a by multipliying an input matrix with a given gain matrix element by element. This is achieved by

Gain<Vector2, Vector2, true> g4({10,20});

The third template parameter specifies an element-by-element multiplication. Please beware of the fact that in this case input signal and gain matrix must be of the same dimensions.

The smooth change feature can be enabled with

Gain<Vector2> gain(10);
gain.enableSmoothChange(true);

Setting a new gain value will now cause the gain to change with small steps towards this new value. The incremental steps can be set with

gain.setGainDiff(0.1);

For some applications, the gain should decrease when the input values exceed a certain limit. You can configure and switch on such a parabolic behavior with

gain.setParabolicLimit(5.0);
gain.enableParabolicGain();

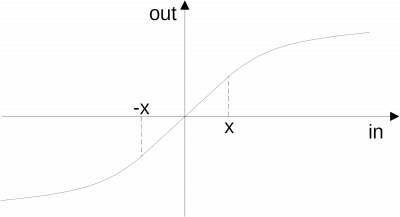
The gain curve then becomes

Within the limits of [-x .. +x] the output value will be calculated simply as

out = k * in; // with k being the linear gain

When the input exceeds this limits the gain will be gradually reduced and the output becomes

out = k * srqt(x * (2 * in - x));